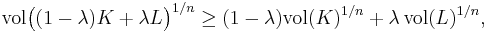Geometric measure theory
In mathematics, geometric measure theory (GMT) is the study of the geometric properties of the measures of sets (typically in Euclidean spaces), including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets. It has applications in various areas, including image processing and fracture mechanics.
Deep results in geometric measure theory identified a dichotomy between rectifiable sets on the one hand and purely unrectifiable or fractal sets on the other. The Compactness Theorem for rectifiable sets, together with deep regularity results, solves for example the Plateau problem—proves that every smooth closed curve in 
bounds a smooth "soap film" or minimal surface, defined as a surface with mean curvature 0. (The earlier result of Jesse Douglas which won him the first Fields Medal in 1936 allowed nonphysical self-intersections.) Later Jean Taylor [1] after Fred Almgren proved Plateau's laws for the kind of singularities that can occur in more general soap films and soap bubbles clusters.
Some basic results in geometric measure theory can turn out to have surprisingly far-reaching consequences. For example, the Brunn-Minkowski inequality for the n-dimensional volumes of convex bodies K and L,
can be proved on a single page, yet quickly yields the classical isoperimetric inequality. The Brunn-Minkowski inequality also leads to Anderson's theorem in statistics. The proof of the Brunn-Minkowski inequality predates modern measure theory; the development of measure theory and Lebesgue integration allowed connections to be made between geometry and analysis, to the extent that in an integral form of the Brunn-Minkowski inequality known as the Prékopa–Leindler inequality the geometry seems almost entirely absent.
See also
References
- Federer, Herbert (1969), Geometric measure theory, series Die Grundlehren der mathematischen Wissenschaften, Band 153, New York: Springer-Verlag New York Inc., pp. xiv+676, ISBN 978-3540606567, MR0257325
- Federer, H. (1978), "Colloquium lectures on geometric measure theory", Bull. Amer. Math. Soc. 84 (3): 291–338, doi:10.1090/S0002-9904-1978-14462-0, http://www.ams.org/bull/1978-84-03/S0002-9904-1978-14462-0/
- Gardner, Richard J. (2002), "The Brunn-Minkowski inequality", Bull. Amer. Math. Soc. (N.S.) 39 (3): 355–405 (electronic), doi:10.1090/S0273-0979-02-00941-2, ISSN 0273-0979, MR1898210, http://www.ams.org/bull/2002-39-03/S0273-0979-02-00941-2/
- Mattila, Pertti (1999), Geometry of Sets and Measures in Euclidean Spaces, London: Cambridge University Press, pp. 356, ISBN 978-0521655958
- Morgan, Frank (2009), Geometric measure theory: A beginner's guide (Fourth ed.), San Diego, CA: Academic Press Inc., pp. viii+249, ISBN 978-0-12-374444-9, MR2455580
- O'Neil, T.C. (2001), "Geometric measure theory", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=G/g130040